机器学习
线性回归
线性回归需要训练集 训练集包括输入输出 确定目标输入的向量即每个输出对应的输入的维度 列对应的拟合线性方程 确定合适的损失函数 以损失函数的标准来优化拟合方程
代价函数是所需要确定的参数的函数 损失函数计算的是当前训练集中所有样本的损失要最小化的是所有样本的损失
代价函数可以自己定义只要符合一定要求 能转化为最优化问题 进而用sgd Gd更新时需要同时更新参数 假设初始化参数时将其放在了局部最优点 他将不会去更新
随着gd进行计算更新的幅度降低因为越接近最低点斜率越低如果起始位置不对或者学习率 不合适则会导致发散在极点附近来回摆动最后越来越大
对于训练集中特征如果每种特征在数值表示上的值相差较大则cost函数图形会很不规则 将每类特征做归一化 或者减去均值让其分布在一定范围 这样可以让梯度下降不会太慢
- 保证每个分量的梯度都相对一致
分类问题
终于知道为什么代价函数需要写成(x-y)的平方了:为了构造成凸函数类似于2次函数一样的图形 用互熵损失的时候,用sigmoid函数作为激活函数时计算得到的结果类似与回归问题的损失函数不同点在于因为是log形式的所以求导的时候多出ln(10)这一项 除了gd还有ocnjugate gradient ,BFGS ,L-BFGS
多分类问题
多分类的损失函数 先将预测结果在每一类上求损失和再求所有样本上的损失和 先将样本种类表示成0 1 的形式在将输出结果表示成每一类的百分比,
Over—fiting
正则化在代价函数上增加关于自变量的平方 所以在减小代价函数的时候有必要减小正则化项(参数值越小函数就越平滑)通过正则化项缩小了所有的参数值
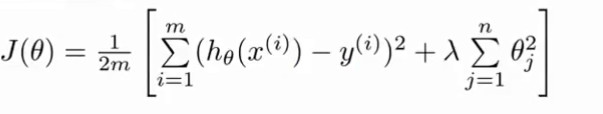
损失函数增加后面那一项 λ是正则化参数(针对所有参数进行正则化) 当正则化 过于严重时会出现欠拟合状态因为要降低损失函数所以正则化项趋于0 参数都趋于0 会导致生成一条平稳直线 加入λ就是为了防止欠拟合 例如:当λ取一个很大的值时需要对权值大大的减小 这样得到的方程将会很平滑出现欠拟合状态
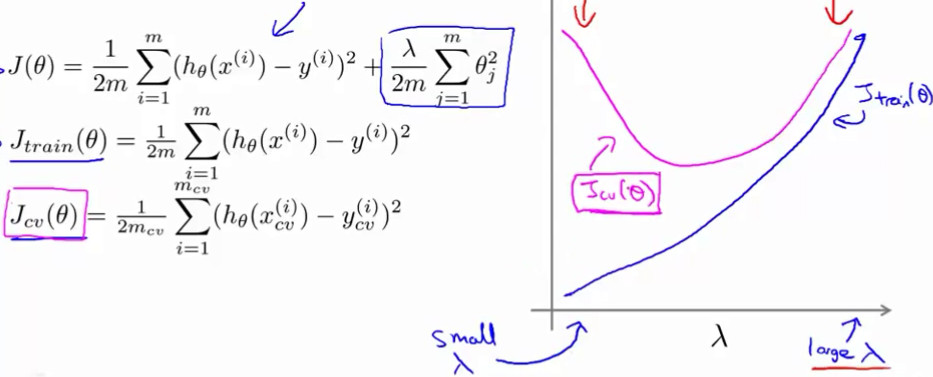
训练集损失:当λ很小时过拟合状态所以损失很小当λ很大时欠拟合状态损失很大 交叉验证集:当λ很小时过拟合所以在验证集上表现不好损失很大随着λ逐渐增加验证集损失开始减小到达最小点时合适 再增加由于欠拟合验证集损失开始增加
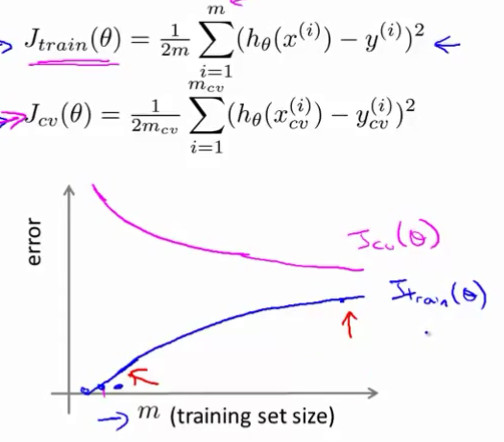
训练集规模也会影响损失函数的变化
跟新参数的方程
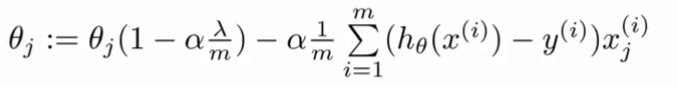
神经网络的损失函数
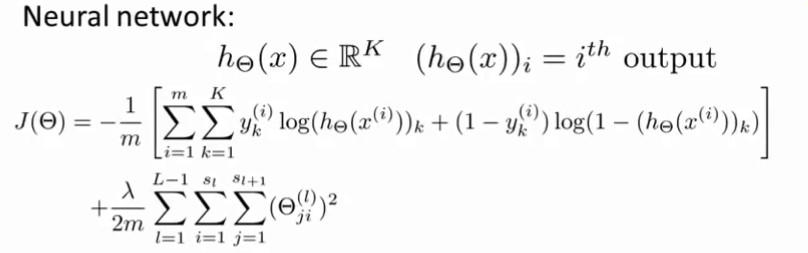
用互熵损失函数k表示输出单元的个数(每个单元都是0到1)m是样本数量 后面一项是正则化项 对所有权重求正则化 (对输出的每个神经元求互熵损失加起来构成一个样本的损失 在将所有样本损失加起来构成整个神经网路的cost)
- 用交叉验证集来选取函数网咯模型
- 在训练集上的损失和交叉验证集上的损失 当两者都很大时说明是欠拟合状态
- 当只有交叉验证集损失较大时时过拟合状态
设计机器学习系统的问题
样本中种类个数有很大差距时,当系统只能预测数量大的那一类时正确率很高但是却不是符合事实的分类器
构造算法前需要选择合适的模型
- 查准率 例如:预测某类结果正确的个数与所有的我们预测得到该结果的个数之比(表示预测的准确性很高)
- 召回率 例如:预测某类结果正确的个数与所有实际该类的个数之比(表示保证不会漏掉) 高查准率高召回率是好的模型

