回归 svm 损失函数 神经网络 机器学习

机器学习应用层理解2

Posted by 高庆东 on September 6, 2017

Svm

核函数问题

核函数将原来特征映射到其他坐标中

高斯核函数 表示了与给出的特征的相似程度

Svm多分类问题

对于有多个类有两种方法进行分类方法1：针对每个类分别建立一个分类器只用于区分 该类和其他类，将测试样本输入每个分类器 输出最大值即对应该类 （可能出现的问题：计算出来的值都是负数，或者一样大）

方法2：对于k个种类针对每两类建立一个分类器 一共有看k*（k-1）/2个分类器每两类对应一个分类器 将测试样本输入所有分类器中计算样本被分到每一类的次数 得票多的即为分类结果（可能出现的问题是如果有得票次数一样多的怎么办）

  • 问题1对于少training多featuer的训练集醉汉使用线性核函数（也就是不用核函数）
  • 问题2对于少featuer多training的训练集使用高斯核函数

非监督学习

K_means：初始化k个中心针对每个样本分别计算到k个中心的距离选择距离最近的中心作为该样本的种类 将所有样本遍历一遍后 重新计算聚类中心 继续迭代

（问题：当有个聚类中心没有任何一个样本是属于该类的）

K-means优化函数

局部最优化问题

解决办法：尝试多次初始化聚类中心（初始化为训练样本中的某k个样本） 通过多次初始化聚类中心用优化函数来衡量选择哪个聚类结果

如何选择聚类个数 没有明确的算法来对k值进行预测

降维问题

####Pca过程 1 去均值化： 将m个样本的每个维度求均值会得到n个均值然后用每个样本的n个特征减去均值

2 构建矩阵 构建正定矩阵 矩阵为n*n维的（n为每个样本的特征维度） 求所有m个样本构建的矩阵的均值

3奇异值分解 U矩阵为n*n的矩阵

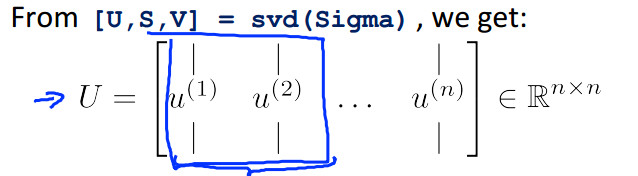
奇异值分解

将n维降到k为的过程中首先选择U矩阵的前k列构造成新举证Uk Uk为nk的矩阵 降维后的特征向量Zi=Uk的转置Xi(Xi为原来的样本的特征向量)（i表示第i个样本） Xi的维度是n*1

选取主成分的个数

S矩阵是对角矩阵特征值，元素的大小表示了所占的成为的比重

比重大小

（减少特征维度可以防止过拟合）

异常检测

给出训练样本集（不需要带标签）计算训练样本分布 给出测试样本 如果测试样本不在 训练样本的分布范围内 则该测试样本属于异常 通过训练集建立一个模型x的概率模型

对于异常检测算法首先估计样本的分布规律满足那种分布（高斯分布式最常见的分布）

对于每个样本的概率 都是关于其每维特征的联合分布（假设每维都是独立同分布的）所以每个样本的概率等于该样本每维特征的概率的乘积，假如每维特征都是服从高斯分布的针对所有样本每一维求均值和方差，

其算法如下

异常检测算法

  • 对于算法的评定：需要用有标签的数据进行评定

  • 异常算法和监督学习算法的对比：异常算法中正负种类的个数相差较大 而监督学习中种类的个数比较均衡

  • 对于样本中某个特征不服从高斯分布：将该特征取对数或者开方 化为高斯分布

异常检测中的问题：

样本的概率分布是圆形的 只能判断圆形区域的异常情况 下图中绿叉属于异常红叉非异常但是绿叉每一维特征的分布都是相对较好的 所以相乘也是非异常但是事实上绿叉属于异常 只用一维的高斯分布最终样本的分布是圆形的 同一个圆上的样本具有相同的概率分布

建立联合分布函数

  • 单一的高斯分布的方差值可以构成多元函数的方差矩阵的对角线 如果所有的特征之间是独立的关系时则两种异常算法等同

  • 用下面方法捕获不是直观的异常需要自己创建新特征 例如：两个特征的比值

  • 而多元模型不需要它可以自动捕获异常

  • 多元模型中方差举证必须是可逆的若果不可逆则样本中存在相关的特征 或者样本的个数m小于特征维度n

推荐系统

对于有n个用户m个商品用户推荐问题如下求未未评价的电影的分数（该算法是基于知道每部电影的特征）

类似与线性回归，针对每个用户都拟合一条直线 Θj表示第j个用户的参量

最小化目标函数的过程：化为最小化所有用户的目标函数 用梯度下降法来训练参数

特征学习 通过对数据的统计用已知的样本去学习样本特征的过程

用梯度下降去求解x和θ

（通过已知数据学习出样本的特征和权重 针对某类商品根据用户选择让机器自己去总结该商品具有的特征和权重）（不知道该设置多少维的特征向量）通过用户之前的结果再结合商品的特征给用户推荐商品

对于大数据样本算法

####随机梯度下降

随机梯度下降针对每个样本的损失函数求梯度将所有权重更新一次直到将所有样本都遍历一遍算一轮更新 特点：单个样本更新所有权重，所以从整体的损失函数看的话会权重的更新可能是震荡的 ，经常会陷入局部极小点 ，当样本很大时相当于进行了很多次的更新所以 更新的轮次只需要几次就够了 一轮更新可以很大程度上趋近最优点（图中紫线所示）

梯度下降算法需要求所有样本整体的损失 用整体的损失求梯度，每轮更新只更新了一次梯度所以需要很多轮的更新他的走势趋近于平滑的线（图中红线） 但是每轮更新计算了所有样本的多轮的更新大大增加了时间消耗

更新算法

梯度跟新算法

Mini_batch_size

用随机梯度下降用cost函数来观察 每进行1000次的cost函数更新则画出这1000次更新cost的平均值 （如果发现cost函数呈现上升趋势可能是因为学习率太大了） （自动减小学习率会出现两种现象：1学习率减小在接近最优点的时候梯度也在减小导致整体学习速度大大降低 2减小学习率可以控制每一步更新不会跨过最优点，不会在最优点附近摆动）

在线学习算法

每有一个数据 用该数据进行参数的调节（用梯度下降法或者什么的） 调节完后将该数据抛弃，再进来新的数据后接着调节，如此进行下去。 例子：一个物流网站，用户通过查看需要收取多少邮费选择寄还是不寄，多少邮费就是y值 用户可以选择寄件地址收件地址 重量 大小等这就是x值的特征 针对所有选择寄件的用户看成是回归模型，给出合理的寄件费用 。每有一个寄件用户就对模型更新一次

Map_reduce 计算方法 只是将数据简单的分开来算

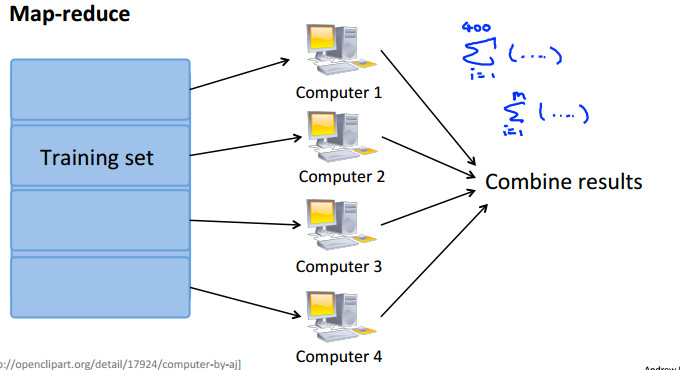
MapReduce

假如有400个数据需要对数据进行梯度计算 可以分来计算每组数据的梯度然后 汇总起来送给下一步 需要确定的是：算法需要的数据可以表示成求和的形式

CATALOG
    FEATURED TAGS
    c语言 c++ 面向对象 指针 容器 python 函数 数据结构 回归 损失函数 神经网络 机器学习 似然函数 极大似然 标准化 深度学习 卷积网络 参数估计 beta分布 数据处理 gradio 模型工程化 网页 模型加速工具 c++实现 变量 占位符 tensorflow 线性回归 学习tensorflow HMM RNN 强化学习 LSTM pandas 不定长序列损失 pytorch 目标检测 RPN 非极大值抑制 ROIpooling VGG16 Transformer BERT Python 装饰器 方法 Pytorch FPN 图像分类 CNN 多模态 生成 GPT Tranformer 生成模型 audio