一些值得注意的问题

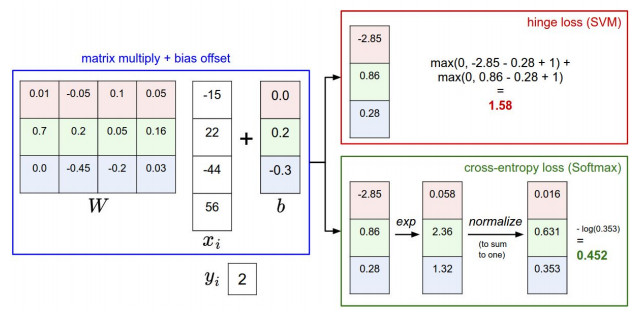
规范化数据
去均值和归一化 在图像去均值时可以是通道上的也可以的像素上的
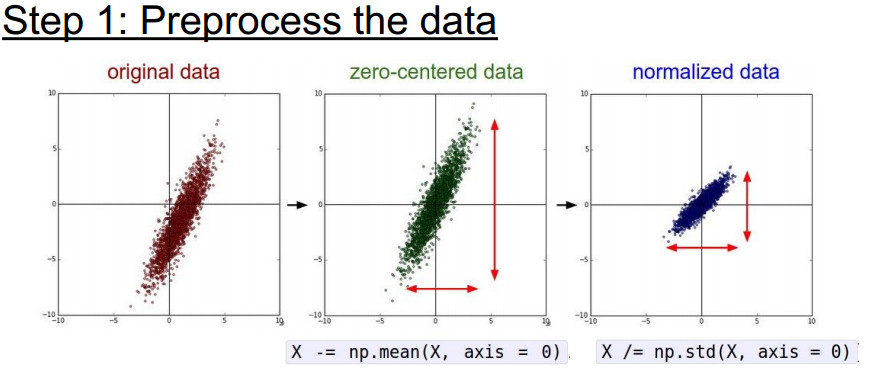

更新参数的方法详解
1 momentum update 基于对梯度的方向改变
SGD每次更新的时候只更新了一个batch的方向当另一个batch来的时候方向就变了 会在山谷间来回摆动向前 就像一个没有质量没有摩擦力的球只会沿着梯度方向走 最终导致来回摆动下面的梯度方向不是最优点的方向
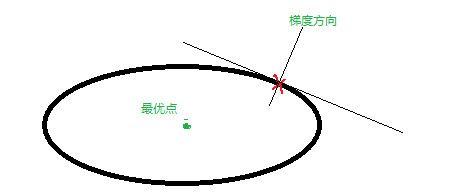
加入动量后增加了摩擦力减小了来回摆动的现象 让动量相互抵消摆动的作用

V可以初始化为0 对于mu开始时梯度会很大可以选取小的mu 当梯度减小时再选择小mu 简单来说:目标是一致的都是朝像最优方向更新理论上只需要沿一个方向走就能很快的 到达最优点SGD是沿着梯度方向走但是梯度方向中包含了最优方向 加上mu项后会 抵消掉一部分其他方向的能量
基于学习率的修正
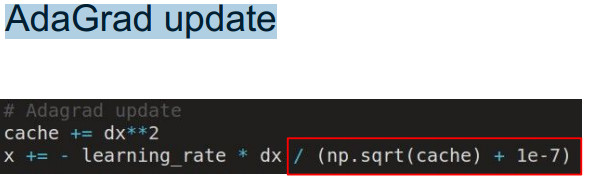
对于每个参数都对应一个学习率 自动适应每个参数的更新幅度 学习率变为一个向量依赖的是每个梯度的情况 随着梯度的更新cache项会逐渐增大 (因为是平方项总和永远不会减小)对应学习率逐渐减小 类似与正则化减小过拟合 有利于解决梯度消失和梯度爆炸问题:梯度小学习率大 梯度大学习率小

二阶牛顿法

二阶牛顿法可以精确求解最优解
原理:求损失函数的最优解就是求一阶导数为零的点 将函数做二阶泰勒展开,对展开式的参数求导求解出参数值
Dropout
让神经网络只记住一部分东西 比如:一只猫不用记住猫的所有特征只需要记住非常有特点的特征 一个神经元开启概率是0.5 所以所有输出的可能的平均值时将所有可能结果加起来取均值 意0.5 的概率将神经网络组合成了很多结构每个结构可以预测一个输出 然后取均值相当于 网络模型有很多对于预测的结果也有很多 取均值后泛化了数据

卷积网络的小问题
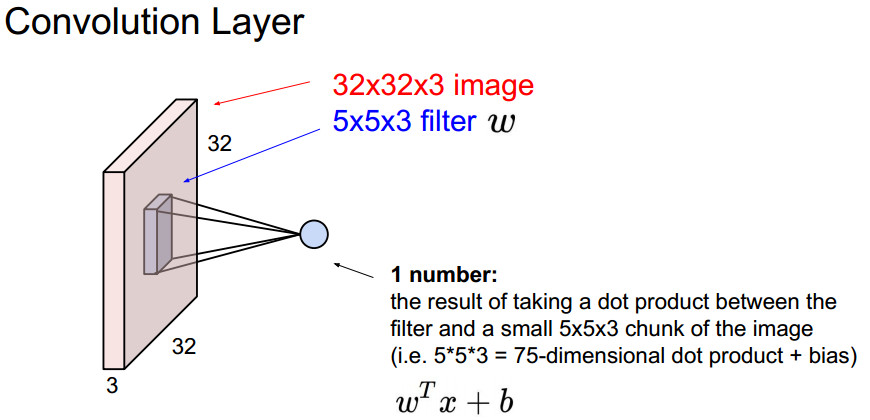
- 一个filter对应一个偏置
- 卷积的图像,大小收缩的太快效果会很差
卷积层与全连接层的连接:全连接层相当于卷积核大小同上层的featur map 一样大进行卷积全连接层的神经元的个数自己定义
假如:卷积层有6个feature map 大小是55 设全连接层有10个神经元则参数总数为6(55)10+10
