激活函数
- tanh比sigmoid更长梯度更大
- relu函数有大梯度通过时可能使神经元死掉
数据集
对于初始的模型数据很少的情况下可以人为增加数据
对于初始模型数据只要存在一点点的差别都会人为是完全不同的数据
最主要的是去掉不需要的数据
(旋转,缩放 裁剪,平移)
样本特征的相关性除了政府相关外还有其他的复杂的相关性
协方差举证:对角线是自身的方差,其他事两两的协方差
如果独立 cov(x,y)=0 如果con(x,y)=0则不相关
pearson系数
数据样本间的线性关系强度在-1到1之间0表示不相关
spearman系数
用于不服从正太分布的资料数据,对两列数据分别排序然后取原始数据 的位置信息作为新数据计算pearson相关性。spearman相关专门用于计算等级数据之间的关系,这类数据的特点是数据有先后等级之分但连续两个等级之间的具体分数差异却未必都是相等的,比如第一名和第二名的分数差就未必等于第二名和第三名的分数差。两次考试的排名数据适用于spearman相关
计算方法
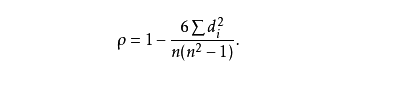
其中di表示两列数据的距离
- 样本很少时不能把均值当做期望
UCB方法
平均收益只是对实际收益期望的一个估计 采样较少的时候均值会与期望产生较大的偏离
疑问
推荐系统偶尔的推荐可以是错误推荐吗?
KL距离
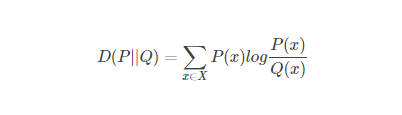
可以将该距离定义为损失函数
p(x)未知有样本x1.。。。xn设q(x)与p(x)相似则损失函数可以定义为kl距离
拉格朗日问题
设 minf(x) g(x)<0 h(x)=0
L(x,v,u)=f(x)+vg(x)+uh(x)
L函数可以是非凹凸的但其对偶函数y(v,u)一定是凹的
- 逻辑回归的本质是样本看成两点分布的最大似然估计
- 线性回顾的本质是误差函数看成高斯分布的最大似然估计
- 牛顿法的学习率是1但是要求初始点相对靠近最优点否则会适得其反
- 熵:不只是混乱度,是最优选择,等于1的概率熵最小等于1/2熵最大
FEATURED TAGS
c语言
c++
面向对象
指针
容器
python
函数
数据结构
回归
损失函数
神经网络
机器学习
似然函数
极大似然
标准化
深度学习
卷积网络
参数估计
beta分布
数据处理
gradio
模型工程化
网页
模型加速工具
c++实现
变量
占位符
tensorflow
线性回归
学习tensorflow
HMM
RNN
强化学习
LSTM
pandas
不定长序列损失
pytorch
目标检测
RPN
非极大值抑制
ROIpooling
VGG16
Transformer
BERT
Python
装饰器
方法
Pytorch
FPN
图像分类
CNN
多模态
生成
GPT
Tranformer
生成模型
audio