EM算法
相当于寻找聚类中心的过程
1假设样本是个服从混合分布,混合了几个或者混合的分布都不知道
2其中的超参数有 几个分布,什么分布
3假定参数已知,列极大似然函数
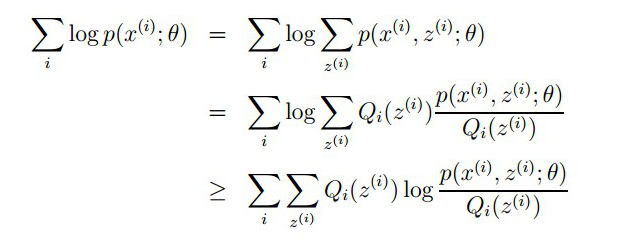
4根据jensn不等式设置循环条件
5让不等式无线趋近于等式,最终得到循环
在样本分类问题中
- 假设参数计算类别
- 根据类别再估计参数
- 根据参数再再修正类别
极大似然(MLE)极大后验(MAP)贝叶斯
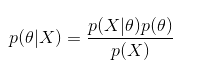
极大似然
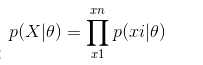
首先假设样本独立然后求极值。求极值的意义在于求使发生这些样本下
最大概率下参数值。
最大后验
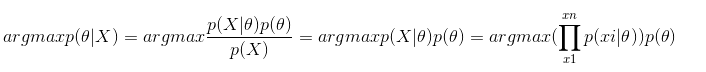
在极大似然的基础上乘参数的先验概率,在样本较少的情况下非常实用
二项分布的参数是事件发生的概率,这个参数的分布符合beta分布
是共轭分布。
- 二项分布的共轭分布是beta分布
- 多项式分布的共轭分布是狄利赫里分布
- 所谓共轭分解就是先验分布和得到的后验分布属于同一分布
贝叶斯
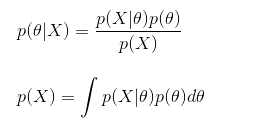
分母p(x)不能忽略,他的用作有归一化
在某个参数下样本发生的概率与样本发生时这个参数的概率有线性关系
FEATURED TAGS
c语言
c++
面向对象
指针
容器
python
函数
数据结构
回归
损失函数
神经网络
机器学习
似然函数
极大似然
标准化
深度学习
卷积网络
参数估计
beta分布
数据处理
gradio
模型工程化
网页
模型加速工具
c++实现
变量
占位符
tensorflow
线性回归
学习tensorflow
HMM
RNN
强化学习
LSTM
pandas
不定长序列损失
pytorch
目标检测
RPN
非极大值抑制
ROIpooling
VGG16
Transformer
BERT
Python
装饰器
方法
Pytorch
FPN
图像分类
CNN
多模态
生成
GPT
Tranformer
生成模型
audio