自相关系数 AR模型 MA模型 时间序列 平稳序列

时间序列模型

Posted by 高庆东 on July 13, 2018

自相关系数

对于时间序列将序列拆分成两列，按照一定的规则（滞后一段时间）

表示同一序列过去与现在的关系

 x1 x2 x3 x4 x5 x6 x7 x8 x9 x10 原始数据
 x1 x2 x3 x4 x5 x6 x7 x8  滞后2个单位
 x3 x4 x5 x6 x7 x8 x9 x10 生成第二列数据

与求相关系数的公式类似

自相关

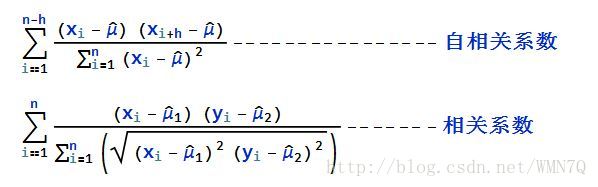
公式1中的均值为总体的均值公式2中的均值为两个序列的均值

AR（自回归模型）

和线性回归类似的方程只不过其阶数表示需要过去多少个时间点

AR模型

需要考虑的因素有

1平稳性：平稳序列的方差均值与时间无关 其特征函数的根在单位圆内，特征函数就是用回归系数构造的方程的解是在单位圆内

2自相关系数：将模型以不同的滞后单位分解成n对序列，每对序列求一个自相关系数，可以构造一个系数图，

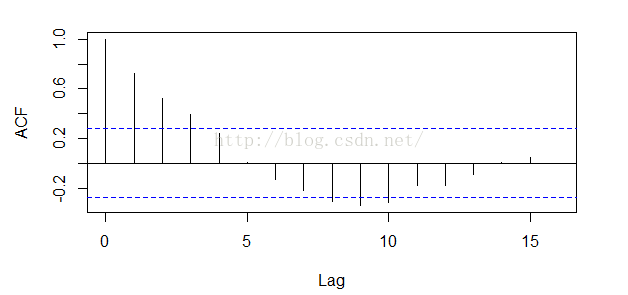
自相关系数图

这是个例子当滞后等于0的时候自相关系数为1 依次有滞后系数0到15滞后单位下的自相关系数

AR模型的阶数是个超参数求解AR模型的方法有

  • 最小二乘法
  • yulr-walker

MR(噪声拟合)

与AR模型类似AR模型由不同阶的滞后序列拟合而MA模型由不同阶的 噪声拟合

ARMA

AR模型与MA模型的合并

CATALOG
    FEATURED TAGS
    c语言 c++ 面向对象 指针 容器 python 函数 数据结构 回归 损失函数 神经网络 机器学习 似然函数 极大似然 标准化 深度学习 卷积网络 参数估计 beta分布 数据处理 gradio 模型工程化 网页 模型加速工具 c++实现 变量 占位符 tensorflow 线性回归 学习tensorflow HMM RNN 强化学习 LSTM pandas 不定长序列损失 pytorch 目标检测 RPN 非极大值抑制 ROIpooling VGG16 Transformer BERT Python 装饰器 方法 Pytorch FPN 图像分类 CNN 多模态 生成 GPT Tranformer 生成模型 audio