HMM 前向后向算法 RNN 语音识别

RNN+softmax构成的ctc算法

Posted by 高庆东 on November 12, 2018

解决的问题

时序数据的分类问题 传统时序训练数据数据需要做对齐处理，这个工作耗时费力

本文提出的方法是不需要做数据对齐的 在RNN网络末尾加上CTC层

可以实现不等长的标签训练模型

实现

首先在RNN网络最后 一层是softmax层这层除了标签数据外加一个空格输出

结合前后向算法设置一个合理的损失函数，CTC本质是一个损失函数的创意

评价函数

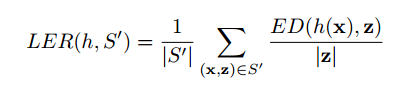
LER函数

这个函数是用来评价模型的性能 ED(h(x),z)表示模型输出与实际值的差值

差值计算时最小编辑距离，再除标签长度，再除样本集大小

β函数

首先这个函数是一个是一个转换函数，因为有空格的假如所以在最后需要将

空格去掉，这个函数是用来去掉输出的标签中重复的和空格，

路径概率

路径概率

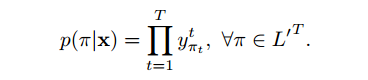
在softmax层某时刻输出的是标签矩阵中的某个值的概率，所有时刻的输出

构成一个路径，（假设输出是独立的）所有时刻的输出构成一个路径，这个

路径就是最终某个标签的一种可能，把所有可能的路径概率加起来，构成

这个标签的概率

分类器函数

CTC分类器函数

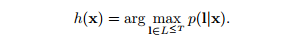
这个函数给出最优分类标签，这个函数很难求数值解，有两种方法求近似解

1找到最可能路径，最可能路径对应最可能标签序列，

2用动态规划的思想来求解，首先求解某个时间段的最优解

网络的训练推导

首先定义两个前向和后向变量

前向变量

后向变量

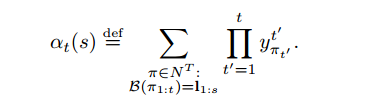
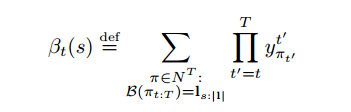
这两个变量是用动态规划的思想推导出来的 前向变量需要第一个转移概率

后向变量需要最后一个转移概率。转移的情况有三种 转向空格和本身和下

一个标签，

损失函数定义为

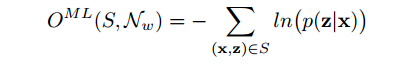
CTC损失函数

最大化概率和函数即最小化负对数损失

针对每个softmax的输出字符求导，使用的技巧是前后向算法的推导结果带

入上式，得到在某个时刻的所有路径，将所有时刻概率加起来构成最终输出

公式如下

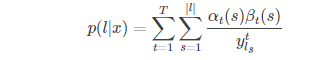
CTC最终概率形式

CATALOG
    FEATURED TAGS
    c语言 c++ 面向对象 指针 容器 python 函数 数据结构 回归 损失函数 神经网络 机器学习 似然函数 极大似然 标准化 深度学习 卷积网络 参数估计 beta分布 数据处理 gradio 模型工程化 网页 模型加速工具 c++实现 变量 占位符 tensorflow 线性回归 学习tensorflow HMM RNN 强化学习 LSTM pandas 不定长序列损失 pytorch 目标检测 RPN 非极大值抑制 ROIpooling VGG16 Transformer BERT Python 装饰器 方法 Pytorch FPN 图像分类 CNN 多模态 生成 GPT Tranformer 生成模型 audio