Focla loss
从交叉熵说起
y表示标签值
y_表示模型输出值
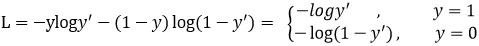网络的输出只有一个，此时输入是正样本的时候 希望输出y比较大
Log(y)就会接近0 损失就很小，当此时的输入是负样本的时候，
希望输出y比较小 此时log(1-y)也会很小。所以完全符合我们的预期
正样本希望输出比较大负样本希望输出比较小，
当正样本过来时输出y非常大时损失非常小 此时非常容易确定是正样本，
当输入负样本的时候的时候输出y非常小此时可以很容易确定是负样本
这样模型只能区分开容易区分的数据。对于中间部分的时间很难区分。
这时可以限制区分容易数据的能力，去提高区分不容易区分数据的能力
加一个限制因子就可以了
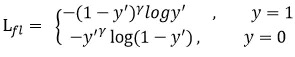可以看到当输入是正样本时模型得到的y如果非常大，那说明模型可以轻易区分
这样的数据，所以对于这个的训练就减少些，乘（1-y）后损失的占比会更小
当输入是负样本的时候如果得到的y非常小，说明模型可以很容易区分这部分数据。
所以再乘一个很小的y，让这部分的训练损失在小一些，减少训练
L1 loss
$\ell(x, y) = L = {l_1,\dots,l_N}^\top, \quad$
$l_n = \left| x_n - y_n \right|$
N表示batch size
L1在0点位置不平滑导数不存在，切导数一直是常数，会在极值点附近波动，
L2导数平滑导数因为导数为2x，再初始位置比较大，所以初步训练时不稳定
梯度结果是常数不管预测值和真实值的差值大小如何变化，反向传播时其梯度不变。
除非调整学习率大小，不然每次权重更新的幅度不变。理想中的梯度变化应该是：训练初期值较大，
则梯度也大，可以加快模型收敛；训练后期值较小，梯度也应小，使模型收敛到全局（或局部）极小值。
L1 Loss 优点：梯度值稳定，使得训练平稳；不易受离群点（脏数据）影响，所有数据一视同仁。
L1 Loss 缺点：0点处不可导，可能影响收敛；值小时梯度大，很难收敛到极小值（除非在值小时调小学习率，以较小更新幅度）。
在线性回归中使用L2损失实际是噪声是高斯分布的最大似然估计
CrossEntropyLoss
1、取log再去softmax 再取负对数
2、权重随类别变化
$l_n = - w_{y_n} \log \frac{\exp(x_{n,y_n})}{\sum_{c=1}^C \exp(x_{n,c})}$
SmoothL1Loss
TripletMarginLoss
$L(a, p, n) = \max {d(a_i, p_i) - d(a_i, n_i) + {\rm margin}, 0}$
d表示计算距离函数
a表示锚点例如搜索任务中的query
p表示正样本例如搜索中被用户点击的资源
n标书负样本例如搜索任务中未被用户点击的资源
